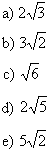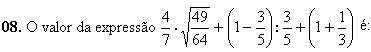Radiciação

O termo radiciação pode ser entendido como uma operação que têm por fim, fornecida uma potência de um número e o seu grau, possa determinar esse número.

Este tutorial fica um pouco mais prático, pois como já estudamos em tutoriais anteriores sobre potências, caso não tenha estudado sugiro que revise. A radiciação resumindo e sendo objetivo é inverso da potenciação.

Exemplo, quando elevamos um determinado número X à sexta potência e depois em uma operação de extração de raiz na sexta potência, temos como resultado o número X.

- Exemplos para fixação de conteúdo

1) Ache a raiz cúbica do número 27 (3√27). Devemos nos perguntar qual o número que multiplicado por ele mesmo três vezes resulta o número 27, ou seja, determinar qual o número que elevado na potência 3 resultado o número 27 ?

Resposta:

É o número 3 , pois sendo: 33 = 3 x 3 x 3 = 27

2) Ache a raiz cúbica do número 64 (3√64), devemos nos perguntar qual o número que multiplicado por ele mesmo três vezes resulta o número 64, ou seja, determinar qual o número que elevado na potência 3 resultado o número 64 ?

Resposta:

É o número 4 , pois sendo: 43 = 4 x 4 x 4 = 64

01) (UFRGS) O valor da expresão é:

    (A) -4
    (B) 1/9
    (C) 1
    (D) 5/4
    (E) 9

02) (UFRGS) A expressão é igual a:

    (A)

    (B)

    (C)

    (D)

    (E)

03) (UFRGS) O valor de para e

    (A)

    (B)

    (C)

    (D)

    (E)

04) (UFRGS) Sendo n > 1, a expresão é equivalente a:

    (A)

    (B)

    (C)

    (D)

    (E)

05) (PUC-RS) A expressão é igual a:

    (A) 164
    (B) 83
    (C) 82
    (D) 45
    (E) 41

06) (UFRGS) Simplificando encontramos:

    (A)

    (B)

    (C)

    (D)

    (E)

07) (UFSM) O valor da expressão é:

    (A) 3.10³
    (B) 3
    (C) 3.10
    (D) 9.10³
    (E) 27.10³

08) (UFSM) O valor da expressão é:

    (A)

    (B)

    (C)

    (D)

    (E)

09) (UFRGS) Assinale a relação correta, das citadas abaixo.

    (A) se a > 1
    (B) se 0 < a < 1
    (C) se 0 < a < 1
    (D) se 0 < a < 1
    (E) se a > 0

10) O valor da expressão

    (A)
    (B)
    (C)
    (D)
    (E)

11) Qual o valor da expressão:

para n pertencente aos naturais - {0, 1}

    (A) 5
    (B) 1/5
    (C) 1/25
    (D) 5²
    (E) 5º

12) (FUVEST) Dos números abaixo, o que está mais próximo de

    (A) 0,625
    (B) 6,25
    (C) 62,5
    (D) 625
    (E) 6250

01 - E

02 - E

03 - C

04 - A

05 - E

06 - B

07 - C

08 - A 

09 - C

10 - A

11 - C

12 - E